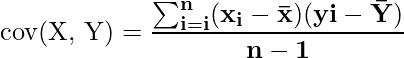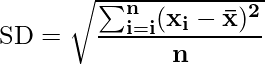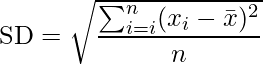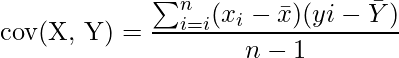Formula, Meaning, Types, and Analysis

It is crucial to examine the useful value or real-world effect of the findings in addition to the analytical significance of the findings when researching or examining speculative information. The concept of impact magnitude is then pertinent in this circumstance. Scientists can measure and talk about the application of their findings by utilizing the standardized procedure of impact size to explain the size of the observed impact.

Approximating and comprehending impact sizes rely greatly on impact size solutions. These formulas are meant to condense the magnitude of distinctions in between groups or the strength and instructions of the link in between variables. Scientists can increase the reproducibility of their findings, much better comprehend the significance of their discoveries, and make sensible judgments by determining the impact size.

What is Impact Size?

The Idea of “impact Size” in stats determines the degree or strength of a relationship in between 2 variables or the difference in between 2 groups. It shows just how much a specific treatment, intervention, or element affects a wanted outcome. The impact size is useful since it makes it possible for academics and specialists to comprehend the useful value or real-world worth of their findings.

What is Impact Size Formula?

We utilize Cohen’s D technique to calculate how carefully 2 variables relate:

Impact Size = (M1– M2)/ SD

where,

M₁ is the mean of the very first population group,

M₂ is the mean of the 2nd population group, and

SD is the basic variance.

Analysis of Impact Size

Impact Sizes: Utilizing standardized requirements, impact sizes can be divided into 3 classifications: little, medium, and huge. Many meanings of small, medium, and big impacts might apply depending upon the scenario and the research study subject.

In addition to analytical significance, impact size likewise adds to evaluating the useful value or worth of the outcomes. An outcome might not constantly have a huge effect size even if it is statistically substantial, and the reverse is likewise real. Both analytical and useful significance needs to be thought about while taking a look at information.

Kinds Of Impact Size

Impact Sizes are categorized into many types, The intent of each of which is to determine the relationship in between 2 variables. The most secondhand kinds of impact sizes are:

Cohen’s d
Pearson’s r
Chances Ratio
Phi Coefficient

Let’s talk about these enters information as follows:

Cohen’s d

The standardized distinction in between 2 methods is determined in this.

Cohen’s d = M₁— M₂/ SD

Where,

d is the efficient size,

M₁ is the mean of the very first population group,

M₂ is the mean of the 2nd population group, and

SD is the basic variance.

SD = â {(SD₁² + SD₂²) â 2}

Where SD₁ and SD₂ are the Basic variance of very first and 2nd popilation group.

Pearson’s r

It Determines how highly 2 variables are associated linearly.

Pearson’s r = cov( X, Y)/( SD_x Ã SD_y)

Where,

cov( X, Y) is covarience in between Xand Y,

$bold{text{cov(X, Y)} = {dfrac{sum_{i=i}^{n} (x_i-bar{x})(yi-bar{Y})}{n-1}}}$

SD_x is basic variance of X, and

SD_y is basic variance of Y.

$bold{text{SD} = sqrt{dfrac{sum_{i=i}^{n} (x_i-bar{x})^2}{n}}}$

Chances Ratio

This determines the possibility that an occasion will happen in one group vs another and is offered as follows:

Chances Ratio = (a/b)/( c/d)

Where a, b, c, and d are frequencies of 2 Ã 2 table.

Phi Coefficient

This determines how highly 2 binary variables relate, and mathematically offered by:

Phi Coefficient = (advertisement– bc)/ â {(a+ b)( c+ d)( a+ c)( b+ d)}

Where a, b, c, and d are frequencies of 2 Ã 2 table.

Fixed Examples of Impact Size Formula

Example 1: 2 groups of trainees’ test outcomes were compared in a research study. Group B got a typical rating of 85 whereas Group A got a typical rating of 80. The pooled basic variance was determined as 10. Identify the impact size utilizing Cohen’s d.

Response:

Provided: M₁ = 80, M₂ = 85, and SD = 10

Utilizing the formula, d = (M₁— M₂)/ SD

â d = (80– 85)/ 10

â d = -5/ 10= -0.5

The impact size, in this case, is -0.5.

Example 2: A standardized stress and anxiety scale was utilized in a research study to compare the stress and anxiety levels of 2 groups. Group X scored approximately 35, whereas Group Y scored approximately 40. The determined pooled basic variance was 6.5. Utilizing Cohen’s d, identify the impact magnitude.

Response:

Provided: M₁ = 35, M₂ = 40, and SD = 6

Utilizing the formula, d = (M₁— M₂)/ SD

â d = (35– 40)/ 6.5

â d = -5/ 6.5 â -0.769

The impact size for this research study is roughly -0.769.

Example 3: Think about 2 groups of trainees, Group A and Group B, with the following marks in a GFG contest. Identify the impact size utilizing Cohen’s d.

Response:

Action 1: First of all we need to identify Mean of 2 Groups

By accumulating the marks for each group and dividing by the overall variety of trainees, we can initially identify the mean for each group:

Group A’s mean (M₁) is (78 + 82 + 85 + 90 + 73)/ 5 = 81.6

Group B’s mean (M₂) is (65 + 70 + 68 + 75 + 72)/ 5 = 70

Action 2: Here we are expect to determine the basic variance.

For Group A: Varience Of Group A: 33.840

Group A’s basic variance (SD_x) is 5.817.

For Group B: Varience Of Group B: 11.6

Group B’s basic variance (SD_y) is 3.406.

Action 3: computing pooled basic variance (SD)

Utilizing the formula for the pooled basic variance

SD = â {(SD₁² + SD₂²) â 2}

â SD â 4.77

Action 4: Figuring out the impact size utilizing Cohen’s d.

For Cohen’s d: Distinction = M₁— M₂ = 81.6– 70 = 11.6

d = Distinction/ SD = 11.6/ 4.7665 = 2.434

The impact size, for this contrast of Group A and Group B mathematics examination ratings is approximately 2.434.

Example 4: Determine Pearson’s r utilizing the info listed below:

X: 1, 2, 3, 4, 5
Y: 2, 4, 6, 8, 10

Response:

As $text{SD} = sqrt{dfrac{sum_{i=i}^{n} (x_i-bar{x})^2}{n}}$

Hence, SD_x = 3, and SD_y = 6

and $text{cov(X, Y)} = {dfrac{sum_{i=i}^{n} (x_i-bar{x})(yi-bar{Y})}{n-1}}$

â cov( X, Y) = 4

And, r = cov( X, Y)/( SD_x Ã SD_y)

â r = 4/ {3 Ã 6}

â r = 4/18

â r = 0.222 …

Example 5: For the following info, identify the chances ratio:

Group 1: 20 success, 30 failures
Group 2: 20 failures, 30 accomplishments

Response:

Odd Ratios of info is; OR = (20/30)/ (30/20) = 4/3

Example 6: Identify the phi coefficient for the offered info:

a = 10, b = 20, c = 30, d = 40

Response:

phi = (1040– 2030)/ sqrt(( 10 + 20 )( 30 + 40 )( 10 + 30) *( 20 +)) phi = 0.22.

Frequently Asked Questions on Impact Size Formula

Q1: Which Impact Size is Perfect?

Response:

The research study’s setting will identify an appropriate impact size. Usually speaking, an effect size of 0.2 is considered small, 0.5 as medium, and 0.8 or above as huge.

Q2: How should Impact Size be Analyzed?

Response:

The research study’s context impacts how impact size need to be analyzed. A bigger impact size generally signifies a more powerful connection in between 2 variables or a higher space in between 2 groups.

Q3: What differentiates Statistical Significance from Impact Size?

Response:

Impact size determines the size of the distinction in between 2 groups or the strength of the connection in between 2 variables, instead of analytical significance, which examines the possibility that the observed distinction or relationship is not the outcome of opportunity.

Q4: Can Impact Size Have a Bad Impact?

Response:

Impact size can, in reality, be bad. The 2 groups being compared are more comparable than unique when the impact magnitude is unfavorable.

Q5: What Benefit Does Utilizing Impact Size Offer?

Response:

The benefit of utilizing impact size is that it offers a dependable method to assess just how much 2 groups vary or how highly 2 variables are associated. This makes it possible for scientists to assess the impacts of various interventions or treatments in a range of trials.