Coprime numbers are ones with simply one typical consider typical, which is 1. To put it another method, a set of numbers is stated to be co-prime if their greatest typical aspect( HCF) is 1. Co-prime numbers can be specified in a range of methods. You will find out about coprime numbers in mathematics in this short article, in addition to how to identify them utilizing a couple of simple ideas and methods and some useful examples.
Tabulation |
|---|
|
What are Co-Prime Numbers?
Expect there are 2 favorable integers x and y that are coprime numbers if and just if they share just the number 1 as a typical aspect, with the outcome that HCF( x, y) = 1. The greatest typical aspect (HCF) of co-prime numbers, or a group of numbers or integers, is 1, making 1 their only typical aspect. Fairly prime or equally prime numbers are other names for co-prime numbers. In order to develop co-prime numbers, 2 numbers are needed.

Characteristics of Co-prime Numbers
Co-primes have particular distinguishing attributes that are offered listed below:
- A set of coprime numbers’ Greatest Typical Aspect (HCF) is constantly 1. For example, considering that the integers 4 and 9 are coprime, HCF (4, 9) = 1.
- The outcome of 2 co-primes is constantly their Least Common Several (LCM). For example, the integers 4 and 9 are co-prime. LCM (4, 9) for that reason equates to 36.
- Every number and 1 makes a set of co-prime numbers.
- Due to the reality that 2 even numbers constantly have 2 in typical, they can not both be co-prime numbers.
- Co-prime numbers constantly have co-prime items when totaled. For example, the integers 5 and 9 are co-prime. In this case, 4 + 9 = 13 and 4 * 9 = 36 are coprime.
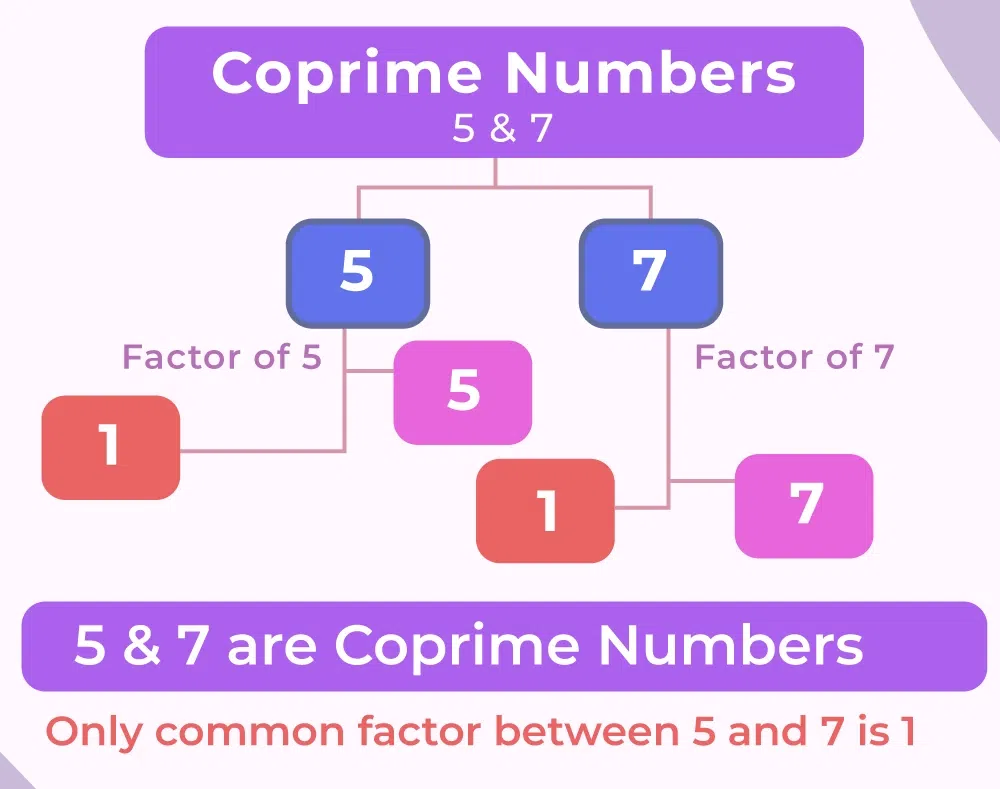
- 2 prime numbers are constantly co-prime. They just share 1 as their typical aspect. Think of 5 and 7. Sole 1 and 5 are the sole prime aspects of 5. The only prime aspects of 7 are 1 and 7. The numbers 5 and 7 are prime. They just share one consider typical: 1. They are co-prime. Any 2 prime numbers can be examined to see if they are co-prime. 2 and 3, 5 and 7, eleven and thirteen, and so on.
- Co-prime numbers are all sets of 2 successive numbers.
How to Discover Co-prime Numbers?
A set of integers is co-prime if there is no other favorable integer (aside from 1) that can divide them both.
For example, 21 and 22
21 and 22:
1, 3, 7, and 21 are the aspects of 21.
1, 2, 11, and 22 are the aspects of 22.
Here, 21 and 22 only share a single aspect, which is 1. Considering that they are co-prime, their HCF equates to 1.

For example, 15 and 20
15 and 20:
1, 3, 5, and 15 are the aspects of 21.
1, 4, 5, and 20 are the aspects of 27.
Here, the numbers 1 and 5 are 2 aspects that 21 and 27 both share. They are not co-prime and HCF is 5.
Co-prime Numbers List
The listed below table reveals the list of co-prime numbers.
| Co prime with | Co-prime numbers sets |
|---|---|
| 1 | ( 1, 2), (1, 3), (1, 4), (1, 5) (1, 6), …, (1, 20), … |
| 2 | ( 2, 3), (2, 5), (2, 7), (2, 9), …, (2, 15), … |
| 3 | ( 3, 4), (3, 5), (3, 7), (3, 10), (3, 11), …, (3, 20), … |
| 4 | ( 4, 5), (4, 7), (4, 9), (4, 11), (4, 13), (4, 15), … |
| 5 | ( 5, 6), (5, 7), (5, 8), (5, 9), (5, 11), (5, 12), … |
Co-primes Numbers from 1 to 100
There are lots of sets of co-primes from 1 to 100 which follow all the above noted homes. Some examples from 1 to 100 are:
( 3, 4)
( 13,14)
( 1, 97)
( 23, 27)
( 29, 31)
( 45, 97) and so on.
We can compose each number in addition to 1 as a co-prime set. In this method, lots of co-prime sets exist from 1 to 100.
Co-prime and Twin Prime Numbers
Co-prime numbers have their HCF as 1. Twin prime numbers, on the other hand, are prime numbers whose distinction is constantly 2. For example, 3 and 5 are twin prime numbers. The differences in between co-prime and twin-prime numbers are noted in the following paragraphs.
- Co-prime numbers can likewise be composite numbers, nevertheless, twin prime numbers are constantly prime.
- Unlike the distinction in between 2 co-primes, which can be any number, the distinction in between 2 twin primes is constantly 2.
- While all co-prime numbers might or might not be twin primes, all sets of twin prime numbers are likewise co-prime.
- Every number and 1 kind co-prime sets, however just 3 and 1 develop twin prime sets.
Fixed Examples on Co-prime Numbers
Example 1: Inspect if 259 and 256 are co-prime numbers.
Option:
Provided numbers are 259 and 256.
1,2,4,8,16,32,64,128 and 256 are the aspects of 256.
1,7,37 and 259 are the aspects of 259.
They just have 1 as their typical aspect for this reason they are co-prime numbers.
Example 2: Inspect whether 28 and 21 are co-prime numbers.
Option:
Provided numbers are 28 and 21.
1,3,7 and 21 are the aspects of 21.
1,2,4,7 and 28 are the aspects of 28.
21 and 28 have 1,7 as their typical aspects. Considering that their greatest typical aspect is 7. Thus, they are not co-prime numbers.
Frequently Asked Questions on Co-Prime Numbers
Q1: What are Co-prime Numbers?
Response:
Coprime numbers are ones with simply one typical consider typical, which is 1. To put it another method, a set of numbers is stated to be co-prime if their greatest typical aspect( HCF) is 1.
Q2: How are prime and co-prime numbers various from each other?
Response:
Prime numbers are those who have just 1 and they themselves as their aspects while co-prime numbers exist in set if the HCF of 2 numbers is 1.
Q3: What is the distinction in between twin prime and co-prime numbers?
Response:
Co-prime numbers have their HCF as 1. Twin prime numbers, on the other hand, are prime numbers whose distinction is constantly 2.
Q4: Are 16 and 37 co-prime numbers?
Response:
The aspects of 16 are 1,2,4,8 and 16.
Whereas the aspects of 37 are 1 and 37.
They just have 1 as their HCF.
Thus they are co-prime numbers.
Last Upgraded:
17 May, 2023
Like Post
Conserve Post